Inverting Fusion Plasmas Improves Performance

The Science

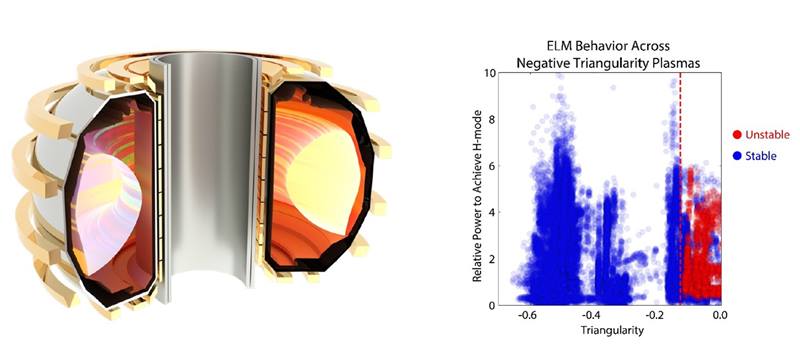
To become commercially viable, fusion power plants must create and sustain the plasma conditions necessary for fusion reactions. However, at high temperatures and densities, plasmas often develop gradients in those temperatures and densities. These gradients can grow into instabilities such as edge localized modes (ELMs). ELMs occur in the plasma edge and have the potential to damage the nearby reactor wall. A feature that can affect ELMs is the cross-sectional shape of the plasma. Researchers use the term plasma triangularity to describe how much the plasma shape deviates from an oval shape. Most studied plasmas have positive triangularity, meaning they have a D-shaped cross-section with the vertical portion of the “D” near the center post of the tokamak. In this research, scientists studied negative triangularity, the inverse shape with the vertical part near the outer wall. Negative triangularity plasmas are known to exhibit some self-regulation of gradients. Through extensive analysis of data from the DIII-D National Fusion Facility program, the researchers showed that this shaping was inherently free of instabilities across various plasma conditions.

The Impact

This research showed that negative triangularity plasmas are free of potentially damaging instabilities in the edge region of the plasma without sacrificing fusion performance. This suggests that negative triangularity shaping stabilizes instabilities in the plasma edge. At the same time, it achieves the high core performance and edge conditions needed to achieve the burning plasma conditions future fusion power plants will need. This result suggests that negative triangularity shaping could be an ideal approach for fusion power plant design.

Summary

Experiments performed with the DIII-D National Fusion Facility tokamak explored the use of negative triangularity shaping to limit the development of highly unstable and energetic ELMs. The work was part of a larger collaboration on negative triangularity that included almost every institution pursuing fusion research in the United States. While ELMs are common under the high-performance plasma conditions relevant to fusion power plants, the study found that negative triangularity shaping limited the development of temperature and pressure gradients that can grow into ELMs in the plasma edge. Notably, plasmas with strong negative triangularity (less than -0.15) did not show any instabilities, even at the high heating power and core performance that typically cause ELMs. In-depth analysis of an extensive DIII-D dataset representing a range of conditions, including the high core performance and edge compatibility needed for fusion reactors, showed this ELM-free nature consistently. 

This work was enabled by the comprehensive, high-fidelity diagnostics of the DIII-D tokamak, and improvements in modeling helped support the conclusions showing improved stability across the expanded range of conditions. Furthermore, this inherent stability was more robust than the ELM suppression achieved with other approaches, such as resonant magnetic perturbations to suppress ELMs or operation in an ELM-free regime. Thus, negative triangularity shaping has the potential to limit the high-energy, damaging plasma instabilities that are currently a major challenge in fusion power plant design. This indicates that the negative triangularity approach warrants further investigation for application in fusion power plant design.

Contact

A.O. Nelson
Columbia University
a.o.nelson@columbia.edu

Funding

This work was supported by the Department of Energy (DOE) Office of Science, Office of Fusion Energy Sciences, using the DIII-D National Fusion Facility, a DOE Office of Science user facility.

Publications

Nelson, A.O., et al., Prospects for H-mode inhibition in negative triangularity tokamak reactor plasmas. Nuclear Fusion 62 096020 (2022). [DOI: 10.1088/1741-4326/ac8064]

Nelson, A.O., et al., Robust Avoidance of Edge-Localized Modes alongside Gradient Formation in the Negative Triangularity Tokamak Edge. Physical Review Letters 131, 195101 (2023). [DOI: 10.1103/PhysRevLett.131.195101]