New Geometric Model Improves Predictions of Fluid Flow in Rock

Supercomputer validates mathematical approach for describing geological features.

The Science

Deep beneath the Earth’s surface, oil and groundwater percolate through gaps in rock and other geologic material. Hidden from sight, these critical resources pose a significant challenge for scientists seeking to evaluate the geometric state of these fluid flows—that is, how they are arranged within porous rock. A research team used an Oak Ridge Leadership Computing Facility supercomputer to create a geometric model that requires just a few measurements to characterize fluid state in porous rock. This work overcomes a well-known deficiency in previous models.

The Impact

A geometric model validated through supercomputing is paving the way for a new generation of models. These models predict fluid state in porous rock from theory rather than by relying on a historical set of data. With these models, scientists could learn more about large subsurface systems like oil reservoirs, sinks for carbon sequestration, and groundwater aquifers.

Summary

Researchers at Virginia Tech used the 27-petaflop Titan supercomputer at the Oak Ridge Leadership Computing Facility to develop a geometric model that requires only a few key measurements to characterize fluid state in porous rock—overcoming a well-known shortcoming associated with previous models.

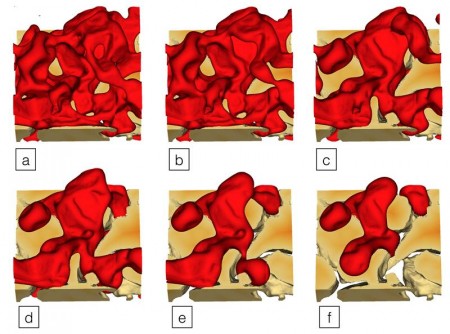
Around the turn of the twentieth century, the German mathematician Hermann Minkowski demonstrated that 3-D objects are associated with four essential measures: volume, surface area, integral mean curvature, and Euler Characteristic. However, in traditional computational models for subsurface flow, the volume fraction provides the only measure of fluid geometry. To apply Minkowski’s result to the complex, multiphase fluid configurations found in porous rock, the Virginia Tech team needed to generate a large amount of data, and Titan provided the extreme computational power needed.

The team selected five micro-computed tomography datasets to represent the microscopic structure of real rocks (such as sand pack and carbonate rock) and a sixth dataset of a simulated pack of spheres. Using its Lattice Boltzmann for Porous Media code, the team simulated and analyzed thousands of possible fluid configurations within each rock, totaling more than 250,000 configurations.

Funding

Army Research Office and National Science Foundation funded this research. Computer time was provided by the Department of Energy (DOE) Innovative and Novel Computational Impact on Theory and Experiment (INCITE) program. This research also used resources of the Oak Ridge Leadership Computing Facility, a DOE Office of Science user facility.

Publications

J.E. McClure, R.T. Armstrong, M.A. Berrill, S. Schülter, S. Berg, W.G. Gray, and C.T. Miller, “Geometric State Function for Two-Fluid Flow in Porous Media.” Physical Review Fluids 3, 084306 (2018). [DOI: 10.1103/PhysRevFluids.3.084306]